Quick Review for Final Exam
TABLE
95% CRITICAL VALUES OF THE SAMPLE CORRELATION COEFFICIENT
| Degrees of Freedom: n - 2 |
Critical Values: (+ and -) |
1
2
3
4
5
6
7
8
9
10 |
0.997
0.950
0.878
0.811
0.754
0.707
0.666
0.632
0.602
0.576 |
Questions 1 – 4 refer to the following:
Sixty (60) De Anza students were asked how many movies (at the movie theater) they saw last month. The data is summarized in the table below.
Number of Movies |
Frequency |
Relative Frequency |
Cumulative Relative Frequency |
0
1
2
3
4
5
6
7
|
10
14
17
7
-
5
1
2 |
0.1667
0.2333 |
-
0.4000 |
| 1. |
What percent of students saw at most 4 movies, approximately? _____________ |
| 2. |
The number of movies is what kind of data? _____________________________ |
| 3. |
The data was collected at De Anza College by dividing all students into 10 groups according to their majors (some groups had more than one major) and then randomly selecting 6 students from each of the 10 groups. The type of sampling is _______________________ |
| 4. |
The average number of movies seen by students in the sample is called the _________________ |
Questions 5 – 8 refer to the following data:
The number of days per week (X) that 100 PE570 students use the exercise facility at De Anza is as follows.
X |
Frequency |
Rel. Freq. |
Cum. Rel. Freq |
0
1
2
3
4
5
6
|
3
12
33
28
11
9
4
|
|
|
5. The 90th percentile is ________________.
6. The average number of days of use is ___________________.
7. The IQR is ____________________.
8. The appropriate box-whisker plot for the data is ___________ (letter)
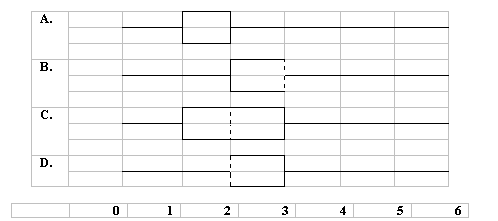
9. The following data are the enrollment (independent variable) at 6 colleges and the number of faculty (dependent variable).
(12,385, 600) (890, 113) (52,895, 3796) (3778, 234) (3023, 144) (800, 63)
The line of best fit is __________________________________.
Is the correlation significant? __________ (YES or NO). The predicted number of faculty for a college enrollment of 65, 000 is 4616 faculty. Does the best fit line give an accurate prediction?_____________ (YES or NO)
Questions 10 – 11 refer to the following:
The California County Average Combined SAT scores (58 scores) for 2002 are shown below:
| frequency |
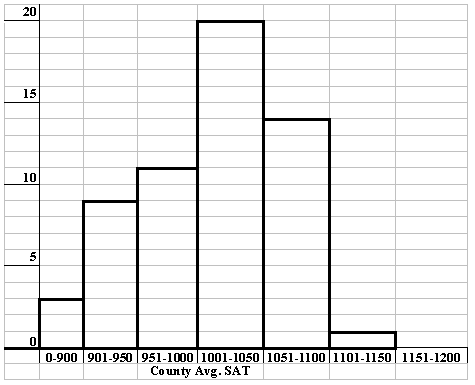 |
10. The number of counties with average SAT scores between 951 and 1050 is __________.
11. The first quartile is between ____________ and ______________
12. Below is the result of the first English 1A exam for three students in three different sections of the course during the fall quarter 2002.
Student |
Score |
Class Average Grade |
Class Average Standard Deviation |
Student 1
Student 2
Student 3 |
75
85
89 |
68
83
90 |
1.5
3
2 |
Who did the best in relationship to his/her class? ____________________________
13. What kind of pattern does the following scatterplot have? ______________________________
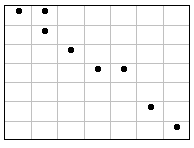
Questions 14 - 15 refer to the following table:
The table shows the performance of the students of three classes taught by a certain Math instructor on the second test. If a student is randomly selected:
|
Math 105 |
Statistics |
Finite Math |
TOTAL |
A
B
C
D
TOTAL |
7
15
12
5
39 |
12
11
8
9
40 |
10
16
11
4
41 |
29
42
31
18
120
|
14. Find P(the student got an A OR the student is in the Statistics class) ________________
15. Find P(the student got a C¦the student is in the Finite Math class)_________________
16. The cost of maintenance on a Toyota Camry during the first year of ownership is exponentially distributed with an average of $350. The probability that a car required more than $700 for maintenance during its first year is ___________________________
17. Given that P(E) = 0.2, P(K) = 0.6, P(E OR K) = 0.7, find P(K|E) _______________
18. Assume the final exam in this course is a 40-question multiple choice exam, with each question having 4 choices, only one of which is correct. Also, assume the questions are answered by random guessing. Let X be the number of questions answered correctly by random guessing. The probability distribution to use is __________________The probability of answering less than 11 questions correctly is ______________________.
19. Assume the daily number of buses running late in the San Francisco metropolitan area follows a Poisson distribution with µ = 7. What is the probability that on any given day there will be more than 7 buses running late? ____________________
20. The average amount of time it takes a person to shower in the morning is 10.5 minutes with a standard deviation of 1.3 minutes. The lengths of showers, in minutes, taken in the morning are known to follow a normal distribution. The probability distribution to use is _________________75% of all showers taken in the morning last at least how long, in minutes_______________________________.
Questions 21 - 22 refer to the following:
The age of a first grader at Talent Elementary School is uniformly distributed from 5.5 to 6.9 years. One student is randomly selected from the class. (Let X = the age of a first grade student at Talent Elementary School).
21. Find P(X > 6.1 years) _______________
22. 30% of the students are under the age of __________________
Questions 23 – 31 refer to the following:
23. In Fall Quarter 2001, 23.8% of all De Anza College students listed "transfer to a 4 year educational institution" as their educational goal. Suppose that for the current quarter, you want to determine whether the percentage of female students who intend to transfer is the same as the percentage of male students who intend to transfer. You randomly sample 100 currently enrolled female students and 100 currently enrolled male students. Conduct a hypothesis test. This is a test of _______________________________
24. Suppose that the average difference between daytime high and nighttime low temperatures are being compared by meteorology students at a college. Twenty days are randomly selected during the term, and for each of those days, the students measure and record both the daytime high and the nighttime low temperatures. This hypothesis test is a test of ___________________________
25. In an issue of USA Today, there were several advertisements for ski areas. Most skiers or snowboarders are interested in finding a reasonably priced room within the ski area. A random sample of the minimum price per night of a room in 7 ski areas is as follows: $35, $65, $65, $79, $89, $99, $99.
Find a 95% confidence interval for the true mean minimum price per night of a room in a ski area.
____________________________________________________
26. A skydiver is preparing to jump out of a plane using a new parachute. Under the assumption that the parachute will open, the Type I error means ________________ (letter)
A. the person jumps and the parachute will not open
B. the person jumps and the parachute opens
C. the person does not jump and the parachute would have opened
D. the person does not jump and the parachute would not have opened
27. As the degrees of freedom increase, the graph of the chi-square distribution looks more and more __________________________________.
28. In a Goodness-of-Fit test, the expected values are the values we would expect if ________________________________________________________________.
29. Use a _________________________ hypothesis test to determine if high school principals believe that students are absent equally during the week or not.
30. The Test for Independence uses a contingency table of expected data values.____________ (YES or NO)
31. The hypothesis test to use when determining if the college or university a student chooses to attend is related to his/her socioeconomic status is a ________________________________.
|