Equipment List:
What you will learn:
This lab teaches how a vernier scale works and how to use it.
I. Introduction:
A vernier scale (Pierre Vernier, ca. 1600) can be used on any measuring device with a graduated scale. Most often a vernier scale is found on length measuring devices such as vernier calipers or micrometers. A vernier instrument increases the measuring precision beyond what it would normally be with an ordinary measuring scale like a ruler or meter stick.
II. How a vernier system works:
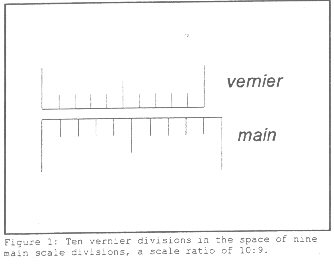
A vernier scale slides across a fixed main scale. The vernier scale shown below in figure 1 is subdivided so that ten of its divisions correspond to nine divisions on the main scale. When ten vernier divisions are compressed into the space of nine main scale divisions we say the vernier-scale ratio is 10:9. So the divisions on the vernier scale are not of a standard length (i.e., inches or centimeters), but the divisions on the main scale are always some standard length like millimeters or decimal inches. A vernier scale enables an unambiguous interpolation between the smallest divisions on the main scale.

Since the vernier scale pictured above is constructed to have ten divisions in the space of nine on the main scale, any single division on the vernier scale is 0.1 divisions less than a division on the main scale. Naturally, this 0.1 difference can add up over many divisions. For example, after six divisions have been spanned by both scales, the difference in length between the vernier and main scale would be 6 X 0.1 = 0.6 divisions.
In figure 2 below, both the vernier and main scale start evenly at the left. After a distance of six increments they differ in length by 0.6 increments as is indicated by the two dotted lines.

In practice, the left sides of the two scales are not matched up as above. Instead, the two left sides of each scale are offset by an amount corresponding to the length measured. In figure 3, the two scales are still off by 0.6 divisions as in figure 2 above, however in figure 3 the scales match up along the dotted vertical line on the right side instead of matching up on left side as in figure 2. In figure 3, we would say the two dotted vertical lines on the left side of the figure are separated by 0.6 divisions of length in the same sense that the two lines in figure 2 are separated by 0.6 divisions. Study and compare figures 2 and 3 to understand how a vernier system works.

III. Measuring an object's length the vernier way:
In measuring the length of an object with vernier calipers, the first two significant figures are read from the main scale. Find where the left edge of the vernier scale crosses the main scale and record the corresponding values immediately so you don't forget them. In figure 4 on the next page, you should confirm that the first two significant figures of the measurement are 2.7 units. This information could be obtained without using a vernier; this is just standard measuring procedure. It is the third significant figure that must be obtained using the vernier scale.
In figure 4, see that the vernier and main scale divisions align where the vernier scale reads 0.4. Actually, in terms of the total instrument this corresponds to a value of 0.04 units, not 0.4. Thus, the measurement of the box's length would 2.74 units.
See that the first two numbers are read from the main scale and the third number from the vernier. Confirm the full measurement in figure 4.

IV. Using the vernier calipers provided: In figure 5 below, the relation between the vernier and main scale is not one of ten in the space of nine but of twenty in the space of nineteen. This increases the precision of the instrument.


V. The absolute uncertainty of your vernier calipers: You will note a 1/20 mm (one
twentieth of a millimeter) printed on the right side of the main scale. 1/20
mm corresponds to 1/200 of a centimeter or in decimals, 0.005 cm. Take this
value to be the absolute uncertainty in your scale reading, although some
people prefer to use 0.003 cm instead, the choice is yours. Below in figure
6, the reading to three significant figures would be 4.26 cm. But notice
the two increments between the vernier and main scale are not perfectly aligned.
You should interpolate the vernier scale to read to three decimal
places. Confirm the reading to be about (4.259 ± 0.005) cm and see
that it is not 4.261 cm since the left-side zero mark on the vernier scale
is closer to the left side zero on the main scale and so the reading
is smaller in value than 4.260.
VI. Making your own vernier scale:
1. Take two 3 X 5 cards provided by your instructor.
2. Using your ruler and a sharp pencil, mark the top edge of one card once every centimeter starting from the left edge of the card all the way to the right side. The very left edge of this card will be the "zero". Every centimeter mark after the zero will be labelled 1, 2, 3, and so on. Write at the bottom of this card: "MAIN SCALE". Examine figure 7 for a rough idea of what you are to do.
3. Take the second card and place it before you on the lab table. At the bottom of this card mark an increment every nine millimeters starting at the left most edge. Mark ten increments only, each separated by nine millimeters. Label each increment with a 1, 2, 3, and so on until you reach 10. Label this card "VERNIER SCALE".
4. You have made your first (and last?) vernier scale which will measure an interpolation of the main scale to a tenth of a centimeter (one millimeter). For one more significant figure, you could interpolate the vernier scale as well.
Use your hand made vernier to measure a few straight lines that you draw into your lab book. Confirm the measurement with your vernier calipers with the measurement from a meter stick. Place the left edge of your MAIN SCALE card at the left edge of the line. Then place the left edge of your VERNIER SCALE at the right edge of the line. Record the length of the line to two decimal places in centimeters (i.e., 2.34 cm).