|

Lesson 2.4 Variance and Standard
Deviation
Variance
The variance is the average of the squares of the
deviations. A deviation is the difference between
a value and the mean and is written as:
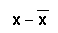
Example: {2, 3, 5, 6} is a set of data. The
sample mean is 4. The deviations are:
2 - 4 = -2
3 - 4 = -1
5 - 4 = 1
6 - 4 = 2
The deviations squared are:
(-2)2 = 4
(-1)2 = 1
(1)2 = 1
(2)2 = 4
An average of the deviations squared is
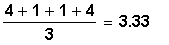
rounded to 2 decimal places. This is the sample
variance. We divide by 3 instead of 4 because, if
we add all the deviations
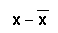
their sum is exactly 0. Knowing 3 of the
deviations determines the 4th one. Only 3 of the
squared deviations can vary freely (can take on
different values). So we average all the
deviations squared by dividing by 3. The number 3
is called the degrees of freedom of the variance.
For a population variance, divide by the total
number of values in the population.
The sample variance is represented by s2
and the population variance is represented by the
Greek letter σ2.
Standard Deviation
The standard deviation is a
special average of the deviations. It measures how
the data is spread out from its mean.
The standard deviation is the square
root of the variance and has the
same units as the mean. The letter s
represents the sample standard deviation and the
Greek letter σ represents the
population standard deviation.
Example: In the variance
example above, the sample variance was s2
= 3.33 (to 2 decimal places). The
sample standard deviation is s =
size="+1">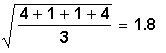
rounded to one decimal place.
NOTE: The standard deviation is the measure that
we use for spread. We use technology to do this
calculation. In today's world, the standard
deviation is almost never calculated by hand
because technology is so easy to use.
Back to Top
Think About It
We can relate a value of the data to its sample
mean and its sample standard deviation by the
equation:
value = mean + (#ofSTDEVs)(standard deviation)
where #ofSTDEVs is the number
of standard deviations the value is from the mean.
For example, if a value of data is 7, its mean is
5, and its standard deviation is 2 then,
7 = 5 + (1)(2)
#ofSTDEVs = 1. The equation reads as "seven
equals five plus one times two." What the equation
means is that the value 7 is 1 standard deviation
above or to the right of (1 multiplied by
2) the mean 5.
Now, suppose in the same data set, we wanted to
know how many standard deviations (#ofSTDEVs) the
value 3 is from its mean. Solve the following
equation for #ofSTDEVs:
3 = 5 + (#ofSTDEVs)(2)
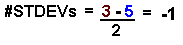
The first equation reads as " three equals
five plus the number of standard deviations times
two." If we solve for the number of standard
deviations (the second equation), we get negative
one as the answer.
Because #STDEVs is negative, we say that the
value 3 is 1 standard deviation below or to
the left of the mean 5
Example: Using the same mean and standard
deviation, calculate how far the value 8.5 is from
the mean
8.5 = 5 + (#ofSTDEVs)(2 )
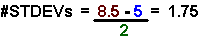
The first equation reads as "eight point five
equals five plus the number of standard deviations
times two." If we solve for the number of standard
deviations (the second equation), we get one point
seven five as the answer.
Because #STDEVs is positive, we say that the
value 8.5 is 1.75 standard deviations above or
to the right of the mean 5.
Example
How to
standardize scores is an important use of
the #STDEVs formula. Close the window when you are
finished viewing the example and you will return
here
We often ask what value is within 1 standard
deviation of the mean, within 2 standard
deviations of the mean, or within 3 standard
deviations of the mean. To find, say, the value
that is within 3 standard deviations of the mean,
we would add to the mean and subtract from the
mean 3 multiplied by the standard deviation.
Example: If the mean is 5 and the standard
deviation is 2, what values are within 3 standard
deviations of the mean?
Calculate:
(5 + (3)(2) = 11 and 5 - (3)(2) = -1 )
The values that are within 3 standard deviations
of the mean are between -1 and 11. Using the same
mean and standard deviation, what values are
within 2.5 standard deviations of the mean?
Descriptive Statistics Problem
Using the TI-83
Example
The next
example is a review of how to use TI-83 or
TI-84 calculators to calculate this Lesson's
descriptive statistics - mean, standard deviation,
median, quartiles, boxplot, and histogram. Please
close the viewing window when you are finished and
you will return here
This is the last section of this
lesson.
Up » 2.1
Graph » 2.2 Quartiles and
Percentiles » 2.3 Mean, Median and Mode »
2.4 Variance and Standard Deviation
|