Lesson 6.3 The Normal Probability Distribution

Examples: Calculating Probabilities and Percentiles

At the beginning of the term, the amount of time a student waits in line at the campus store is normally distributed with a mean of 5 minutes and a standard deviation of 2 minutes.

Let X = the amount of time, in minutes, that a student waits in line at the campus store at the beginning of the term.

Because X ~ N(μ, σ) then, X ~ N(5, 2) where the mean μ = 5 and the standard deviation σ = 2.

Some typical problems using technology (TI-83 calculator):

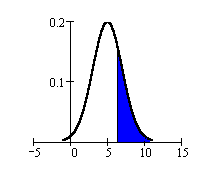
Find the probability that one randomly chosen student waits more than 6 minutes in line at the campus store at the beginning of the term. P(X > 6) = 0.3085. The probability that one randomly chosen student waits more than 6 minutes is 0.3085. This calculation was done using TI-83 or TI-84 calculator function 2nd DISTR 2:normal CDF (6, 1EE99, 5, 2). Find the probability that one randomly chosen student waits between 3 and 6 minutes in line at the campus store at the beginning of the term. P(3 < X < 6) = 0.5328 . 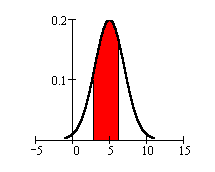The probability that one randomly chosen student waits between 3 and 6 minutes is 0.5328. This calculation was done using TI-83 or TI-84 calculator function 2nd DISTR 2:normalcdf(3, 6, 5, 2) Find the 3rd quartile. The third quartile is equal to the 75th percentile. Let k = the 75th percentile (75th %ile). P(X < k ) = 0.75. 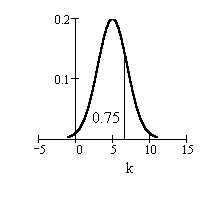The 3rd quartile or 75th percentile is 6.35 minutes (to 2 decimal places). Seventy-five percent of the waiting times are less than 6.35 minutes. This calculation was done using TI-83 or TI-84 calculator function 2nd DISTR 3:invNorm(.75, 5, 2)

Example

The following example is about the percent of calories from fat that a person in the United States consumes. The probabilities and percentile are calculated using TI-83 or TI-84 calculators. Close the window when you are finished viewing the example. You will return here.

Think About It

Do the Try-It examples in Introductory Statistics.

This is the last section of this lesson. When you have completed the assignment and the quiz for Lesson 6, you are ready to begin Lesson 7 - The Central Limit Theorem.

Back to Top

Up » 6.1 Normal Probability Description » 6.2 Standard Normal Probability » 6.3 Normal Probability