Lesson 8.3 Confidence Interval for a Population Mean – Unknown Population Standard Deviation

Notation and Formulae 

Remember that the CI format is:

(point estimate- EB, point estimate + EB)

where EB is the margin of error or error bound.

In a CI for a single population mean where the population standard deviation is unknown, the point estimate is the sample mean and the error bound is the error bound for the mean. So, the CI has the format

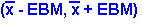
We use the same syntax as we did in the CI for a single population mean where the population standard deviation is known. What is different is how we calculate the error bound EBM.

In the real world, you typically calculate a CI from data. The population standard deviation is not known. In the past, there was no problem in estimating the population standard deviation with the sample standard deviation and using the Central Limit Theorem (when the sample size was large (bigger than 30). Before the general population had access to technology, the Standard Normal Distribution applied. The problem came when the sample size was small. In this case, we use a new distribution called the Student-t, created by William Gossett, its inventor. (Gossett wrote about the Student-t distribution using the pseudonym "Student.")

Now, since we have strong, available technology, we use the Student-t Distribution whenever the population standard deviation is unknown and we are estimating it with s. The sample size does not matter. See Introductory Statistics for a detailed explanation.

The Student-t is a distribution of t-scores (very much like z-scores). If T is the random variable representing t-scores, then the notation for the student-t distribution is:

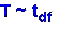
The subscript df is short for "degrees of freedom." it is equal to the sample size - 1.

The equation for a t-score is:

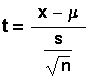
We get EBM similar to the way we get EBM for the case where the population standard deviation is known but we use s in place of >s and t in place of z.

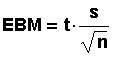
Remember that we subtract from and add to the sample mean to get the CI. In the past, the t-scores were looked up in a very limited table. The limitation was put on the CLl. Today, technology can easily calculate a CI for any CL.

Back to Top

Confidence Interval Problems Using TI-83 or TI-84 calculators

Example: Ten engineers working for start-up companies were asked how long they worked, in hours, per week. The data (in hours) is 70, 45, 55, 60, 65, 55, 55, 60, 50, 55. Construct a 90% CI for the population average length of time, in hours, that engineers at start-ups work per week. Interpret the CI.

The important numbers are the

• the data AND
• 90% confidence interval.

Since we only have data, we use a Student-t distribution. The population standard deviation is not known.

The answer is (52.856, 61.144) using TI-83 or TI-84 calculators.

First, enter STAT 1:EDIT. Then, clear list L1 by arrowing up to the list name, pressing CLEAR, and arrowing down.

Enter the data. The functions to use are:

STAT TESTS 8:Tinterval

Inpt:Data

List: L1

Freq: 1

C-Level: 90

Calculate.

We can interpret the CI in two ways:

• We are 90% confident (or sure) that the population average length of time, in hours, that engineers at start-ups work per week (rounded to 1 decimal place) is between 52.9 and 61.1 hours.
• If we constructed many of these CIs, 90% of them would contain the population average length of time, in hours, that engineers at start-ups work per week.

Example

Most people like French fries. In the example, only data is given so that the population standard deviation is unknown. This example shows you the TI-83 keypad and the keystrokes. Close the window when you are finished viewing the example.

Think About It

• What distribution do we use for a CI for a mean if we only have data? Do we know the population standard deviation?
• If the CL is made smaller, does the CI get larger or smaller?

Back to Top

Up » 8.1 Confidence Intervals » 8.2 Confidence Intervals - Known » 8.3 Confidence Intervals - Unknown » 8.4 Confidence Interval for a Single Population Proportion