Lesson 8.4 Confidence Interval for a Single Population Proportion

Notation and Formulae

Remember that the confidence Interval format is:

(point estimate- EB, point estimate + EB)

where EB is the margin of error or error bound.

In a CI for a single population proportion where the population standard deviation is known, the point estimate is the estimated proportion p' and the error bound is the error bound for the proportion EBP. So, the CI has the format:

Even though we use technology to calculate the CI, we will discuss how we get p', the distribution for the confidence interval, and EBP.

Remember that p' is the point estimate for the unknown population proportion p.

p' is defined as the number of successes, x, in a sample divided by the total, n, in the sample. The equation for p' is:

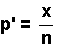
The distribution that is used for the confidence interval is normal. Think back to Lesson 4 and remember the binomial distribution with parameters n and p. p is defined as the probability of a success for any trial (and q is the probability of a failure for any trial: p + q = 1). If X is the binomial random variable, then X ~ B (n, p).

If n is at least 20 and (n)(p) > 5 and (n)(q) > 5, then X has an approximate normal distribution and, as n gets larger, the approximation gets better. In fact, if n is large enough,

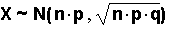
Now, if we take each x of the random variable X and divide it by n, we get estimated proportions. In the distribution above, we must also divide the mean and the standard deviation by n. So,

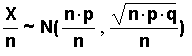
Let X/n = P', the random variable for estimated proportions and we get the distribution:

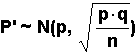
EBP, the error bound for the proportion, has an equation similar to EBM, the error bound for the mean (see the previous two sections, 8.2 and 8.3). Remember that EBM is equal to a z-score or a t-score multiplied by a standard deviation. EBP has a similar format. Since the distribution is normal, we use a z-score. The standard deviation is:

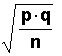
But, we do not know p and q. So, we estimate them with p' and q' and use the estimated standard deviation:

 

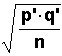
Then,

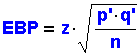
Remember that the z-score depends on the confidence interval.

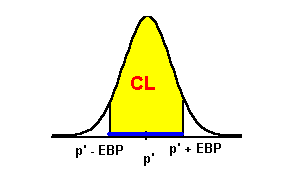
To get the CI, we subtract EBP from p' for the lower value and add EBP to p' for the upper value. The graph illustrates the CI in blue.

Confidence Interval Problems Using TI-83 or TI-84 calculators

Example: In a survey of 80 males, 55 had played an organized sport growing up. Construct a 99% CI for the true population proportion of males who played an organized sport growing up. Interpret the CI.

The important numbers are the:

• sample size of 80,
• number of successes, 55
• 99% confidence interval.

The answer is (0.55401, 0.82099) using TI-83 or TI-84 calculators. The functions to use are

STAT TESTS A: 1-PropZint.

• x: 55
• n: 80
• C-Level: 99
• Calculate

We can interpret the confidence interval in two ways:

• We are 99% confident (or sure) that the true population proportion of males who played organized sports growing up is between 0.55 and 0.82 (from 55% to 82%).
• If we constructed many of these CIs, 99% of them would contain the true population proportion of males that played organized sports growing up.

Example

The following example is about a CI for the true population proportion of families that have children who swim on a swim team at a local cabana club. This example shows you the TI-83 keystrokes. Close the window when you are finished viewing the example.

Think About It

• When a study gives a margin of error of + or- 4 percentage points, this is determined before the survey is done. Since p' and q' are unknown, what is the most conservative choice we can make for them? (You can find the answer in Introductory Statitics.) Why would we make these choices?
• In a survey of 100 taxpayers, 20 feel that a tax rebate is a good idea. What is the point estimate for the true proportion of taxpayers who feel that a tax rebate is a good idea?

This is the last section of this lesson. When you have completed the assignment and the quiz for Lesson 8, you are ready to begin Lesson 9 - Hypothesis Testing: Single Mean and Single Proportion.

Back to Top

Up » 8.1 Confidence Intervals » 8.2 Confidence Intervals - Known » 8.3 Confidence Intervals - Unknown » 8.4 Confidence Interval for a Single Population Proportion