|

Lesson 11.2 Chi-Square Goodness-of-Fit Test
Goodness-of-Fit
In a chi-square goodness-of-fit hypothesis test,
you determine whether or not data "fit" a
particular distribution.
For example, you might want to know if a
particular coin is fair. You could take data by
flipping the coin twice for 100 times. If the coin
is fair, the expected distribution is 25 HH, 25
HT, 25 TH, and 25 TT where H = heads and T =
tails. You could run a chi-square goodness-of-fit
hypothesis test to see if the outcomes from your
data "fit" the expected distribution.
We write the null and alternate hypotheses in
sentences.
Example:
Ho: The coin is fair.
Ha: The coin is not fair.
Notation
The test statistic for a goodness-of-fit test is:
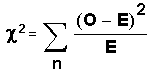
O = the observed values (data).
E = the expected values (the values you would
expect if the null hypothesis were true).
n = the number of different data cells or
categories.
The degrees of freedom df = n - 1.
The test statistic is a measure of how far the
observed values (O) are from the expected values
(E) and is either 0 or positive. If the test
statistic is large, then the observed values are
far from what we would expect if Ho
were true. So, we would reject Ho.
The goodness-of-fit test is almost always
right-tailed.
Hypothesis Testing Problems
Using TI-83 or TI-84 calculators
Example: The percentage of
students who attend a local school in any given
school week is as follows:
|
Monday
|
Tuesday
|
Wednesday
|
Thursday
|
Friday
|
|
95%
|
96%
|
98%
|
97%
|
95%
|
In one given school week, the number
of students (data) who attended school out of a
student population of 500 was:
|
Monday
|
Tuesday
|
Wednesday
|
Thursday
|
Friday
|
|
450
|
470
|
485
|
480
|
470
|
Perform a goodness-of-fit hypothesis test to
determine if the numbers fit the
percentages given.
Formulate the 2 hypotheses.
Ho: The number of students who attend
the local school Monday through Friday fit the
expected percentages.
Ha: The number of students who attend
the local school Monday through Friday do not fit
the expected percentages.
Determine the random variable and the
distribution for the test.
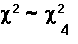
There are 5 cells or categories (Monday, Tuesday,
Wednesday, Thursday, Friday).
df = 5 - 1 = 4.
Using the test statistic calculated from the
data, calculate the p-value.
TI-83 calculator:
- Clear List L1. It will contain the data or
observed numbers ( O). Enter 450, 470, 485, 480,
470.
- Clear list L2. It will contain the expected
numbers (E). Enter the following: 500*.95,
500*.96, 500*.98, 500*.97, 500*.95.
- Clear list L3. Arrow up into the name area
(L3) at the top. Press (L1-L2)2/L2
and ENTER.
- Press 2nd QUIT. Clear the home screen.
- Press 2nd LIST MATH 5:sum(
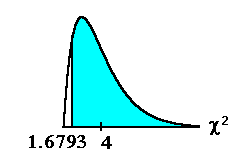
- Press L3) and ENTER. You should see 1.6793 to
4 decimal places. This is the chi-square
test statistic.
- Press 2nd DISTR 7: C2cdf(.
- Enter 1.6793,1EE99, 4). You should see 0.7945
to 4 decimal places. This is the p-value.
Compare α and the p-value and make a decision.
Assume α = 0.05
Since 0.05 < 0.7945 (α< p-value), we do
not reject Ho.
Because the p-value is so large, the test
strongly favors the null hyothesis.
Write an appropriate conclusion.
We conclude that the numbers of students who
attend the local school Monday through Friday fit
the expected percentages.
Example
The following
problem is a chi-square goodness-of-fit
hypothesis testing problem. Close the window when
you are finished viewing the example. You will
return here.
Think About It
Do the Try-It examples in Introductory
Statistics. Verify the numbers. The
calculator instructions follow the problem.
Please continue to the next section of this
lesson.
Up » 11.1
Chi-Square Probability » 11.2
Chi-Square Goodness-of-Fit Test »
11.3 Chi-Square Test of Independence
|