Lesson 3.3 Addition and Multiplication Rules

Addition Rule

A and B are events. The Addition Rule is:

P(A OR B) = P(A) + P(B) - P(A AND B)

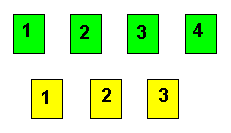
Example: In a box that you cannot see into are three yellow cards numbered 1, 2, 3 and four green cards numbered 1, 2, 3, 4. The experiment is to randomly draw one card.

Let Y = yellow card and G = green card. Each card is equally likely and the sample space is {Y1, Y2, Y3, G1, G2, G3, G4}. There are 7 cards in the sample space.

What is the probability of drawing a green card OR a card with a 1 on it?

There are 4 green cards (G1, G2, G3, G4) and 2 cards with a 1 (Y1, G1). Notice that G1 is repeated.

P(green card) = 4/7

P(card with a 1) = 2/7

P(card that is both green card and has a 1) = 1/7

If G = green card and H = card with a 1, then:

P(G OR H) = P(G) + P(H) - P(G AND H)

P(G OR H) = 4/7 + 2/7 - 1/7 = 5/7

When we add P(G) and P(H), we have counted G1 twice. G AND H refers to card G1. So, when we calculate P(G OR H), we must subtract one occurrence of card G1. That is the reason we must subtract P(G AND H).

Back to Top

The Addition Rule And Mutually Exclusive

If A and B are mutually exclusive,

then P(A AND B) = 0 and the Addition Rule becomes:

P(A OR B) = P(A) + P(B)

Example: A and B are mutually exclusive events. P(A) = 0.05 and P(B) = 0.62. Find P(A or B).

Since A and B are mutually exclusive, the Addition Rule is P(A OR B) = P(A) + P(B) = 0.05 + 0.62 = 0.67.

Back to Top

Multiplication Rule

A and B are events. The Multiplication Rule is

P(A AND B) = (P(A))(P(B |A)) or

P(A AND B) = (P(B))(P(A | B))

Example: P(A) = 0.3, P(B) = 0.12, and P(B | A) = 0.2.

Then P(A AND B) = (P(A))(P(B | A)) = (0.3)(0.2) = 0.06.

Now find P(A | B).

Since P(A and B) = (P(B))(P(A | B)), divide both sides of this equation by P(B). Then,

P(A | B) = P(A and B) / P(B) = 0.06 / 0.12 = 0.5.

Back to Top

The Multiplication Rule and Independence

If A and B are independent, then

P(A | B) = P(A) and P(B | A) = P(B). This means that A does not depend on B and B does not depend on A. The Multiplication Rule becomes:

P(A AND B) = (P(A))(P(B))

Example: Toss 2 fair coins. What is the probability of getting 2 tails?

Since the toss of the second coin does not depend on the toss of the first coin,

P(2 tails) = P(tail AND tail) = (P(tail))(P(tail)) = (1/2)(1/2) = 1/4.

Back to Top

Other Probability Problems

Example

The example illustrates the addition and multiplication rules, mutually exclusive, and independence.

Please continue to the next section of this lesson.

Back to Top

Up » 3.1 Terminology »3.2 Independent or Mutually Exclusive » 3.3 Addition and Multiplication Rules » 3.4 Contingency Tables