|

Lesson 7.3 The Central Limit Theorem for Sums
Notation and
Formulae
X is a random variable with a distribution that
may be known or unknown. Using a subscript that
matches the random variable, suppose
- μX = the mean of X
- σX = the standard deviation of X
If you draw random samples of size n, then as n
increases, the random variable
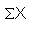
of the sample sums tends to be normally
distributed as follows:
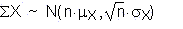
Notice that the mean of the sample sums is equal
to the mean of the original distribution
multiplied by the sample size and the standard
deviation of the sample sums is equal to the
standard deviation of the original distribution
multiplied by the square root of the sample size.

CLT Problems for Sums
Using TI-83 or TI-84 calculators
Example: In 1940, the United States was still
very much a farming nation. The average farm at
that time was 174 acres. Suppose the standard
deviation was 55 acres. We randomly survey 30
farmers from 1940.
Let X = the size, in acres, of one U.S. farm in
1940.

and follows a normal distribution:
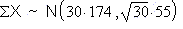
where μX = 174 and σX = 55.
The mean of the sums is (30)(174) = 5220.
Below are some typical problems. The answers have
been calculated using technology (TI-83
calculator).
|
What is the probability that the total
(sum) number of acres of 30 farms in
1940 is more than 5000 acres?
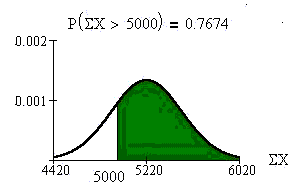
The probability that the total number
of acres of 30 farms in 1940 is more
than 5000 acres is 0.7674.
These calculations were done using the
TI-83 DISTR calculator function 2nd
DISTR.
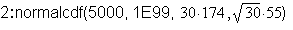
Example: Find the 90th percentile for
the total (sum) number of acres for 30
farms in 1940.
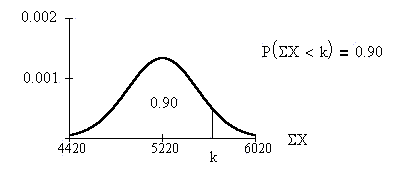
k = 5606.1 acres (to 1 decimal place).
The 90th percentile is 5606.1 acres.
These calculations were done using the
TI-83 DISTR calculator function 2nd
DISTR.
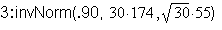
|
Think About It
Do the Try-It examples in Introductory
Statistics.
This is the last section of this lesson. When you
have completed the assignment and the quiz for
Lesson 7, you are ready to begin Lesson 8 -
Confidence Intervals.
Up » 7.1
Central Limit Theorem »
7.2 Central Limit Theorem for Averages »
7.3 Central Limit Theorem for Sums
|