|

Lesson 9.5 The Type I and Type II Errors
Type I Error
A Type I error occurs when we reject Ho
when Ho is really true.
Fixed or pre-conceived α (the same α we used in
hypothesis testing) is the probability of
rejecting Ho when Ho is
really true. So,
α = P(Type I error).
We always try to minimize α.
Example: Suppose Ho is
The coin is fair.
The Type I error is
We do not think the coin is fair when, in fact,
it really is.
So, α = P(Type I error) = the probability that we
think the coin is not fair when, in fact, it
really is.
Example: Suppose Ho is
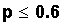
where p is the proportion of Americans who vote
in presidential elections. In words, Ho
is "At most, 60% of Americans vote in presidential
elections."
The Type I error is
We think that the proportion of Americans who
vote in presidential elections is more than 60%
when, in fact, the proportion is at most 60%.
(If we reject Ho, then we think that p
> 0.60.)
So, α = P(Type I error) = the probability that we
think the proportion of Americans who vote in
presidential elections is more than 60% when, in
fact, the proportion is at most 60%.
Example: Suppose Ho is
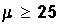
where μ is the average cost, in dollars, of
dinner at the better restaurants in Silicon
Valley.
The Type I error is:
We think that the average cost of dinner at the
better restaurants in Silicon Valley is less than
25 dollars when, in fact, the cost is at least 25
dollars.
(If we reject Ho, then we think that
the average cost is less than 25 dollars.)
So, α = P(Type I error) = the probability that we
think the average cost of dinner at the better
restaurants in Silicon Valley is less than 25
dollars when, in fact, the cost is at least 25
dollars.
Type II Error
A Type II error occurs when we do not reject Ho
when Ho is really false.
We use the Greek letter β as the probability of
not rejecting Ho when Ho is
really false. So,
β = P(Type II error).
We always try to minimize b.
Example: Suppose Ho is
The coin is fair.
The Type II error is
We think the coin is fair when, in fact, it
really is not fair.
So, β = P(Type II error) = the probability that
we think the coin is fair when, in fact, it really
is not fair.
Example: Suppose Ho is
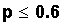
where p is the proportion of Americans who
vote in presidential elections. In words, Ho
is "At most, 60% of Americans vote in presidential
elections."
The Type II error is
We think that the proportion of Americans who
vote in presidential elections is at most 60%
when, in fact, the proportion is more than 60%.
So, β = P(Type II error) = the probability
that we think the proportion of Americans who
vote in presidential elections is at most 60%
when, in fact, the proportion is more that 60%.
Example: Suppose Ho is
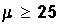
where μ is the average cost, in dollars, of
dinner at the better restaurants in Silicon
Valley.
The Type II error is:
We think that the average cost of dinner at the
better restaurants in Silicon Valley is at least
25 dollars when, in fact, the cost is less than 25
dollars.
So, β = P(Type II error) = the probability
that the average cost of dinner at the better
restaurants in Silicon Valley is at least 25
dollars when, in fact, the cost is less than 25
dollars.
Back to Top
Decision Table
We can summarize the Type I and Type II errors
and the correct decisions in a table.
|
---
|
Ho is true
|
Ho is false
|
|
Do not reject Ho
|
Correct Decision
|
Type II error
|
|
Reject Ho
|
Type I error
|
Correct Decision
|
The Power of the Test is defined to be 1 - β.
1 - β is the probability of rejecting Ho
when, in fact, Ho is really false. It
is desirable to have a high power since we would
always want to reject Ho when Ho
is really false.
Besides being used in the Power of the Test, β is
also used to determine the appropriate sample size
for the hypothesis test. You do not study β
extensively in this course. If you were to take
the next statistics course, you would learn more
about β.
Think About It
To help you better understand the Type I and Type
II errors, do the Try-It examples Introductory
Statistics. You can check some of your
answers in the back of the book.
This is the last section of this
lesson.
Up » 9.1
Hypothesis Testing
» 9.2 Hypothesis Testing -
Known » 9.3 Hypothesis Testing-
Unknown » 9.4 Hypothesis Testing for a
Single Population Proportion »
9.5 Type I and II Errors
|