12.1 Linear Equations

Bivariate Data

Up to this point, you have used single-valued or univariate data. This lesson introduces bivariate data which are two related values of data. Examples include:

• height and weight
  Example: (72 inches, 200 pounds)
  
• the year a person was born and life expectancy
  Example: (1950, 65 years)
  
• your grade on a second math exam and your final exam grade
  Example: (80%, 83%)
  
• education and income
  Example: (4 years of college, $100,000)

You will learn the basics of how to determine if there is a linear relationship between the two values of the bivariate data by understanding the concepts of linear regression and correlation.

Back to Top

Notation

Linear regression for two variables is based on a linear equation of the form.

y = a + bx
where

x is the independent variable,
y is the dependent variable,
and a and b are constant numbers.

Typically, you choose a value for the independent variable x and solve the equation for y.

The graph of a linear equation of this form is a line that is not vertical.

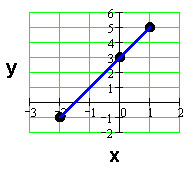
Example: y = 3 + 2x

By substitution:

If x = 1, then y = 5.

If x = 0, then y = 3.

If x = -2, then y = -1.

We can plot the points (1, 5), (0, 3), and (-2, -1) and construct a graph as shown below.

Back to Top

The Slope and Y-Intercept

For the linear equation:

y = a + bx
a = the y-intercept and
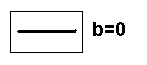
b = the slope of the line

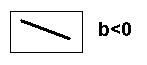
• The slope b describes the steepness of the line (remember the rise/run formula).
• The y-intercept a is the y coordinate of the point (0, a) where the line crosses the y-axis.

Examples:

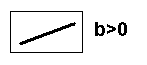
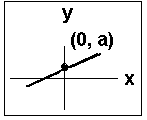
Please continue to the next section of this lesson.

Back to Top

Up » 12.1 Linear Equations » 12.2 Scatter Plots » 12.3 The Regression Equation » 12.4 The Correlation Coefficient » 12.5 Prediction » 12.6 Outliers » 12.7 TI-83